【数理知识】概率论试题（一）

1 确定与随机

问题

设你和朋友玩一个游戏，规则如下：

1、桌子上有7颗棋子，你们二人轮流拿走一定数量，最终谁先拿走最后一颗棋子的人获胜；

2、你的朋友相信随机，在他的回合里，他可以投掷一枚6面子，并拿走对应数目的棋子（如果剩下的棋小于这个数目则全部拿走)；

3、你不喜欢随机，因此在你的回合里可以自行决定拿走1颗棋子或2颗棋子，但是不能不拿，同时你可以选择先走或后走那么在最优决策的情况下你的获胜几率是多少？

解答

首先最优决策的情况一定是选择后手，且每次只拿1颗棋子，除非到你的回合时场上只剩1-2颗棋子，此时可以全部拿走获胜，因为在没有把握决胜时，给对方回合留的棋子越少，你失败的概率更高。

定义轮到你时，如果还剩 $n$ 个棋子，胜率为 $p_n$ 。则易得： $p_1 = p_2 = 100%$

$n=3$ 时，你拿1，对方拿1，你再拿1才能胜利，即： $p_3 = \frac{1}{6}p_1=\frac{1}{6}$

同理 $p_4 = \frac{1}{6}p_1+\frac{1}{6}p_2=\frac{2}{6}$

可以得到规律： $p1=p2=1， p_n=\frac16\sum\limits_1^{n-2}p_i$

所以 $p_{win}=\sum\limits_1^6p_i=\frac{59}{108}$

2 切分三角形

问题

一个等边三角形，一定能够分成n个等腰三角形，其中n大等于3。

解答

首先，我们可以将任意一个等边三角形分为3个120°的等腰钝角三角形；也可以将之分为4个等边三角形。

而其中120°的等腰钝角三角形可以分为2个120°的等腰钝角三角形和一个等边三角形。

所以从图1情况出发，我们一定可以分出2n+1(n≥1)个三角形。

而从图2情况出发，再将其中的等边三角形按照图一方式切割，一定能分出2n(n≥2)个三角形。

两者结合，就证明一个等边三角形，一定能够分成n(n≥3)个等腰三角形。

3 交换次数期望

问题

对于 $n$ 个不相同的数 $a_1,a_2, ..., a_n$ 。用如下算法得到其中最大值 $m$ ：令 $m=a_1$ (算作一次赋值)，依次将 $m$ 与 $a_2,a_3, ..., a_n$ 比较，若 $a_i>m$ ，则令 $m=a_i$ ，求对 $m$ 做赋值操作次数的期望。

解答

令 $E_n$ 为 $n$ 个数时， $m$ 的期望，那么若 $a_n=\max\limits_{i=1}^n(a_i)$ ，那么 $E_n=E_{n-1}+1$ ，若 $a_n\neq\max\limits_{i=1}^n(a_i)$ ，那么 $E_n=E_{n-1}$

所以容易得出： $E_n = \frac{1}{n}(E_{n-1}+1)+\frac{n-1}{n}E_{n-1}$ 并且有 $E_1=1$ ，所以 $E_n=\sum_\limits{i=1}^n\frac{1}{i}$

4 样品检查

问题

假设有200瓶测试样品（每个样品不限量），其中一瓶是有毒的，如果我们的检验试剂混合了有毒的测试样品，在20mm内会变为黑色（没有变色的检测试剂可以重复使用，变色后的不可使用）。试问如果我们想在1h内快速找到有毒的测试样品至少需要多少瓶检验试剂？

解答

1h内一瓶试剂最多可以测试3组，如果这3组都没毒，那么第4组有毒。 $4^3=64<200<4^4=256$ 所以4瓶试剂即可。

为了更好理解这一结论，我们用14个样品来做检验，将他们用4进制方式进行编号如下：

14个：00 01 02 03 10 11 12 13 20 21 22 23 30 31

	试剂1	试剂2
轮次1	10 11 12 13（黑，锁定第一位编号为1）	01 11 21 31
轮次2	不能用了	02 12 22
轮次3	不能用了	03 13 23（三轮都不黑，锁定第二位编号为0）

如此就可以检验出有毒的一瓶，本质上就是依此检验四进制编号的各个位置，哪个“百位”有毒？哪个“十位”有毒？哪个“个位”有毒？最终锁定一组有毒的“个十百”就锁定了有毒的样品。

5 拿取棋子

问题

你和你的朋友玩一个小游戏，每个人轮流从桌上2023枚棋子中拿走2^n个(1,2,4,8,16等等)，拿走最后1枚棋子的人获胜，请问是否存在一个必胜的策略（谁先开始也没有确定)？

解答

1+2=3；2+4=6；4+8=12均为3的倍数，因此，如果我们能保证我们每次拿取后保证剩余3的倍数个棋子即可。

而2023并不是3的倍数，因此我们要先拿（比如4个），那么剩余2019个，是3的倍数，我们就必胜了。

6 相关系数-证明

问题

设随机变量 $X_1, X_2, ..., X_n$ 两两之间的相关系数都是 $\rho$ ，求证： $\rho\geq-\frac{1}{n-1}$

解答

\begin{align*} &\because 0 \leq Var(\sum\limits_{i=1}^nx_i) \\ &\therefore 0 \leq \sum\limits_{i=1}^n{(Var(x_i))} + 2\rho\sum\limits_{i\lt j}(\sqrt {Var(x_i)Var(x_j)}) \\ &\because 2\sqrt{xy} \leq x+y\\ &\therefore 2\rho\sum\limits_{i\lt j}(\sqrt {Var(x_i)Var(x_j)}) \leq \rho\sum\limits_{i\lt j}(Var(x_i)+Var(x_j)) \\ &\therefore 2\rho\sum\limits_{i\lt j}(\sqrt {Var(x_i)Var(x_j)}) \leq \rho(n-1)\sum\limits_{i=1}^n(Var(x_i)) \\ &\therefore 0 \leq (1+\rho(n-1))\sum\limits_{i=1}^n{(Var(x_i))} \\ &\because \sum\limits_{i=1}^n{(Var(x_i))} \geq 0 \\ &\therefore 1+\rho(n-1) \geq 0 \\ &\therefore \rho \geq -\frac{1}{n-1} \end{align*}

7 四因数平方和

问题

对所有的 $n$ ，使得 $n$ 可以表示为其最小四个因数平方值和（注：1也是因数，且因数不必为质因数）

解答

假设 $n$ 为奇数：

则 $n$ 的因数 $a$ 、 $b$ 、 $c$ 、 $d$ 一定均为奇数。

根据题意，有如下关系成立： $n=a^2+b^2+c^2+d^2$ 为偶数，与假设矛盾。

假设 $n$ 为偶数：
那么 $n$ 一定有因数1和2，所以有 $n=1^2+2^2+c^2+d^2=5+c^2+d^2$ 成立，且 $c$ 与 $d$ 奇偶性不同。不妨设 $c$ 为奇数， $d$ 为偶数，那么：
1. 假设 $n$ 不为4的倍数，那么 $n=2*c=1*d$ ，所以 $n=5+c^2+(2c)^2=5(1+c^2)$ ，说明 $n$ 有一个因数5，即 $c$ 最大为5。
  若 $c=3$ ， $n=50$ 不成立；
  若 $c=5$ ， $n=130$ ， $(130=1^2+2^2+5^2+10^2)$ 成立。
2. 假设n为4的倍数，那么 $n$ 有因数 $d=4$ ，即 $n=5+4^2+c^2=21+c^2$ 。
  有 $\frac{21+c^2}{c}$ 为整数，即 $c=3 or 7$ ，带入显然不成立。

综上所述， $n=130$ 。

8 半圆相交

问题

平面上等距离分布着无数条平行直线，随机扔一个半径为 $\frac12$ 的半圆，求半圆和直线相交的概率。

解答

首先计算一条长为1的线段与平行线相交的概率：

P=\frac{\int_0^{\frac\pi2}\sin\theta d\theta}{\frac\pi2}=\frac{2}{\pi}

两个半圆A、B（各自包含边）组合成的圆与直线相交的概率为1。
利用容斥原理计算可得：
$\begin{align} P(A \cup B) &= P(A) + P(B)-P(A \cap B) \\ 1 &= 2P(A)+\frac{2}{\pi} \\ P(A) &= \frac{\pi-2}{2\pi} \end{align}$

9 回归中的系数约束

问题

岭回归和Lasso回归都通过引入正则项控制模型复杂度，它们的正则项有什么区别，有哪些不同的作用？（例如，在特征选择方面：在多重共线性处理方面）

解答

Ridge的正则项 $\frac{\lambda}{2}\sum\limits_{j=1}^p \beta_j^2$ 是L2的，而Lasso的正则项 $\lambda\sum\limits_{j=1}^p|\beta_j|$ 是L1的。两者都相当于在OLS的基础上加了一定前提条件。

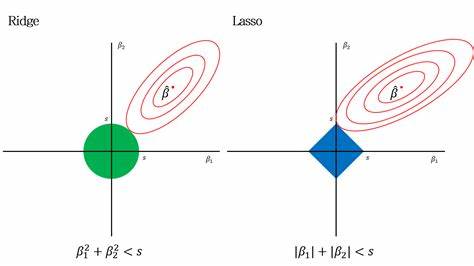
Ridge (L2),&Lasso (L1)

结合上图可得到：Lasso的边界是直线，而Ridge的边界是圆。当最优点不落在边界上时，相当于没有进行正则项约束的OLS方法。当最优点落在边界上时（原有的OLS最佳点在边界外），因为原有的OLS中有平方项，可以看做向外扩张的椭圆，与直线的交点可能在坐标轴上，而与圆的交点则不会。因此Lasso往往倾向于将某些 $\beta_j$ 缩减到0（当 $\lambda$ 足够大时），相当于忽略某些特征，有利于特征筛选和降低模型复杂度：而Ridge不会有这样的能力（特征选择方面）。